Fase

A senóide é a representação gráfica de um movimento oscilante que gerou uma onda mecânica longitudinal transmitida por um meio elástico, através da compressão e descompressão de partes desse meio. Por exemplo o ar.

Fig.1

Como se trata de um movimento alternado – compressão seguida de descompressão – é possível definirmos um ciclo como um movimento completo de onda, sem que haja repetição.

Fig.2

 

Admitindo-se que o ciclo se realiza em intervalos de tempo x, e tomando-se como base a unidade de segundo, dizemos que o período da onda (T) é o tempo gasto para ela completar um Ciclo. (fig2)

A quantidade de ciclos completados pela onda dentro de um segundo é o que chamamos de freqüência.

Fig.3

Portanto: T = 1/F

Alguns exemplos: O período da onda mais grave que somos capazes de perceber (20 Hz) é de 50 ms, pois T= 1/20 = 0,05s ou 50ms.

Da mesma forma o período da onda mais aguda (20KHz) é de 0,05ms. Nos médios temos, por exemplo, o período de freqüência de 1 KHz é igual a 0,001s ou 1ms.

O importante agora é sabermos como produzir filtros acústicos. Para isso precisamos compreender os conceitos de fase e polaridade.

A polaridade pode ser analisada em relação ao primeiro movimento do ciclo da onda.

Fig.4

 

As ondas da figura 4 representam sinais idênticos. No caso C, a polaridade é inversa à do caso B que, por sua vez, é igual à do caso A.

Se somarmos a onda do caso  C com qualquer uma das outras duas, o resultado será zero (ver abaixo), pois onde uma é positiva a outra é negativa e vice-versa.

Fig.5

 

Note que só haverá o cancelamento total se as ondas forem idênticas e somadas a partir do mesmo instante, ou seja, em fase. Assim o que temos na fig.5 são duas ondas em fase, mas com polaridades opostas. A defasagem é relação direta do tempo. Só há defasagem se houver atraso de tempo.

Exemplo: as ondas da figura abaixo estão defasadas, pois não começam no mesmo instante, e conseqüentemente, seus picos e vales não coincidem.

Fig.6

Para compreendermos melhor, vejamos a equação que calcula o desvio de fase:

Ø = t . f . 360º,  onde:

Ø = desvio de fase

t = variação de tempo ou defasagem

f = freqüência

Como estamos tratando de funções senoidais, é conveniente transformarmos o atraso de tempo em ângulo de defasagem para compreendermos melhor a interação de fases.

Fig.7

 

Na figura acima marcamos a onda senoidal com os pontos correspondentes aos principais ângulos de defasagem.

Agora vejamos o que acontecerá com a somatória das amplitudes em cada ângulo. Admita que cada onda, representada nos gráficos a seguir, tem a amplitude original igual a 1 (uma) unidade, que representaremos com a letra U.

Fig.8

 

Quando somamos duas ondas idênticas de amplitude igual a 1U, em fase, ou com defasagem de 360º, o resultado será uma somatória total, com a amplitude resultante igual a 2U. (ver fig.8).

Fig.9

 

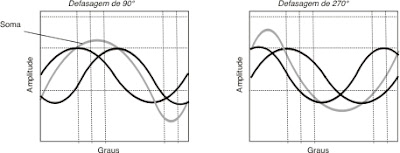
Quando somamos duas ondas idênticas de amplitude igual a 1U, com desvios de fase de 90º ou 270º, o resultado será uma somatória parcial, com aplitude resultande igual a 1,414U. (ver fig.9).

Fig.10

 

E quando somamos duas ondas idênticas de amplitude igual a 1U, com desvios de fase de 120º ou 240º, o resultado será o cancelamento parcial, com amplitude resultante igual a 1U. (ver fig.10)

Fig.11

 

Mas quando somamos dias ondas idênticas de amplitude igual a 1U, com desvio de fase de 180º, o resultado será um cancelamento total, com amplitude resultante igual a zero. (ver fig.11).

Se compreendermos esses conceitos, podemos usar a fase como filtro acústico. Quando você precisar eliminar totalmente uma freqüência, basta usar o cancelamento provocado pela defasagem de 180º. Se deseja apenas atenuá-la, diminua a intensidade de um dos sinais ao somá-los. A vantagem que existe em usarmos a defasagem para equalizar é que não introduzimos ruído ou distorção ao sistema. Além disso, um filtro “notch” acústico pode ser tão eficiente quanto o eletrônico.

Um grande aliado nesses casos é o processamento digital. Um processador com amostragem de 44.1 KHz é capaz de executar uma tarefa a cada 22,68µs. Esse tempo corresponde a aproximadamente metade do período da onda de 20Khz e poderia, portanto, provocar uma defasagem de 180º nessa onda, caso o atraso fosse de um sample (uma amostra). Para maior precisão e controle dessa defasagem, a opção é arranjar um processador com um clock superior a 44.1 KHz. Por exemplo: com 48 KHz 1 sample corresponderia a 20,83µs. Já em 88.22 KHz a menor variação seria de 11,34µs e com 96 KHz de amostragem, a menor defasagem poderia ser de 10,42 µs.