Representação gráfica da função seno (senóide) que, em acústica, também pode representar a onda sonora, através da variação da pressão em função do tempo.
Definições
Ciclo: é o movimento completo da onda sem que haja repetições.
Período: é o tempo gasto para se completar um ciclo.
Freqüência: é o número de ciclos que a onda completa no intervalo de 1 (um) segundo. Portanto, pode ser calculada como o inverso do período: F=1/T
Comprimento de onda: é o espaço percorrido pela onda até completar um ciclo. É representado pela letra λ. Para calcularmos o comprimento da onda, basta dividirmos a velocidade de propagação do som pelo número de ciclo que ela completou em 1 (um) segundo, ou seja, pela freqüência.
Na fórmula: λ = C / F
Amplitude: Representa a intensidade relativa do sinal e pode ser medida de diversas formas. Para nós será eletricamente o valor da tensão (“voltagem”) do sinal de áudio.
1 - amplitude eficaz (RMS) Root Mean Square
2 - amplitude de pico
3 – amplitude de pico a pico
Existem alguns formatos clássicos de onda, entre eles destacamos:
a) Onda quadrada: contém todos os harmônicos ímpares com amplitudes proporcionais sendo que a fundamental sempre tem 100%. Assim, o terceiro deve ter um terço, o quinto um quinto, o sétimo um sétimo e assim por diante.
b) Onda triangular: também contém todos os harmônicos impares, só que com outra configuração de amplitudes.
c) Onda senoidal: é a única que não tem harmônicos.Por isso é chamada de onda pura.
d) Onda serrote: possui todos os harmônicos pares e impares.
Envelope.
O envelope, juntamente com o timbre, determina o som do instrumento. O envelope de onda pode ser descrito como uma variação de volume que ocorre em um intervalo de tempo, enquanto a nota está sendo tocada e que pode variar conforme a execução.
O envelope pode ser composto de 4 (quatro) partes: attack – decay – sustain – release (ADSR)
Há vários fatores (acústicos e eletrônicos) que podem modificar uma onda, criando ou modificando harmônicos que, somados à onda fundamental, determinam o TIMBRE. Entre eles os mais importantes sejam:
a) Fatores acústicos:
- o tipo de material vibrante e/ou ressonante
- a ação vibrante (tipo de vibração)
- as condições acústicas do ambiente.
b) Fatores eletrônicos:
- tipo e quantidade de filtros
- qualidade dos amplificadores de sinal
- fidelidade de resposta dos componentes em relação aos transientes.
Isto porque eles definem justamente a qualidade, o tipo e a fase dos harmônicos que serão somados a onda fundamental.
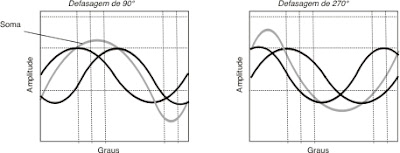
Graficamente:
O som resultante seria a soma da onda fundamental com os harmônicos gerados. Assim, a onda resultante representaria o TIMBRE da fonte sonora.
Ressonância
Considerando-se que todo corpo possui uma massa, podemos dizer que na hipótese dele entrar em movimento oscilante é inerente a esse corpo uma freqüência de oscilação (vibração) que chamamos de Freqüência de Ressonância.
Quando um corpo entra em movimento harmônico, ele faz com que as moléculas de ar que estão a sua volta vibrem na mesma freqüência transmitindo parte de sua energia de vibração para o meio a sua volta, que por sua vez, pode transmiti-la a outro corpo. Se a Freqüência de Ressonância for a mesma para os dois corpos, poderá haver um fenômeno chamado Simpatia. Por exemplo: uma taça de cristal se quebrando apenas com o som de uma nota cantada na mesma freqüência de sua ressonância – pode ser explicado por esse fenômeno.
Numa mola, por exemplo, podemos calcular de forma simplificada a freqüência de seu movimento de oscilação através da formula:
f²= k/m
onde:
f é a freqüência com que a mola vai oscilar
k é a constante de elasticidade da mola
m é a sua massa
Movimento complexo
Quando somamos a um movimento já existente uma nova força de freqüência diferente desta, o resultado é uma somatória de movimentos criando uma resultante bastante complexa. Por outro lado, se a freqüência do novo movimento for igual a freqüência do movimento inicial, o resultado será uma ressonância infinita.
Matematicamente podemos representar esse resultado na fórmula abaixo.
A = a0 / f1² - f2²
Onde:
A é a amplitude da onda resultante
a0 é a amplitude da freqüência já existente
f1 é a freqüência do movimento inicial
f2 é a freqüência que foi adicionada.
Conclusão: o movimento que o alto falante realiza é a somatória de todas as freqüências produzidas.